Forecast Modeling

This tutorial walks through a typical forecasting workflow using LedgerAnalytics. We’ll start by authenticating and connecting to the API

from ledger_analytics import AnalyticsClient

# If you've set the LEDGER_ANALYTICS_API_KEY environment variable
client = AnalyticsClient()

# alternatively
api_key = "..."
client = AnalyticsClient(api_key)

The bermuda library comes equiped with a sample triangle with paid loss and earned premium. It’s a squared triangle running through 1997, so we’ll go through the exercise of predicting ultimate losses as of 1998.

from bermuda import meyers_tri

full_meyers = client.triangle.create(name="full_meyers", data=meyers_tri)

Let’s see which models are available to us for forecasting.

client.forecast_model.list_model_types()

Let’s start with the TraditionalGCC model - which stands for Traditional Generalized Cape Cod. This model is essentially a moving average of the loss ratios from previous accident periods.

gcc_forecast = client.forecast_model.create(
    triangle="full_meyers",
    name="gcc_forecast",
    model_type="TraditionalGCC",
    config={
        "loss_definition": "paid",
    }
)

Now we can predict future losses using this model. We’ll create a triangle that includes which cells we want predictions for, called the “target triangle”. This allows us to specify the periods of the forecast and the earned premium so the models can scale losses and volatility appropriately. Be sure the metadata of the forecast triangle matches the metadata of the training triangle.

import bermuda as tri

target_triangle = tri.Triangle(
    [
        tri.CumulativeCell(
            period_start=date(1998, 1, 1),
            period_end=date(1998, 12, 31),
            evaluation_date=date(2020, 12, 31),
            values={"earned_premium": 5e6},
            metadata=meyers_tri.metadata[0]
        )
    ]
)
target = client.triangle.create(name="target_triangle", data=target_triangle)
gcc_prediction = gcc_forecast.predict("full_meyers", target_triangle=target)

It can be helpful to convert the prediction to bermuda to inspect the results

gcc_prediction_tri = gcc_prediction.to_bermuda()
gcc_loss_ratio = gcc_prediction_tri[0]['paid_loss'] / gcc_prediction_tri[0]['earned_premium']
print(f"Ultimate loss ratio: {gcc_loss_ratio}")

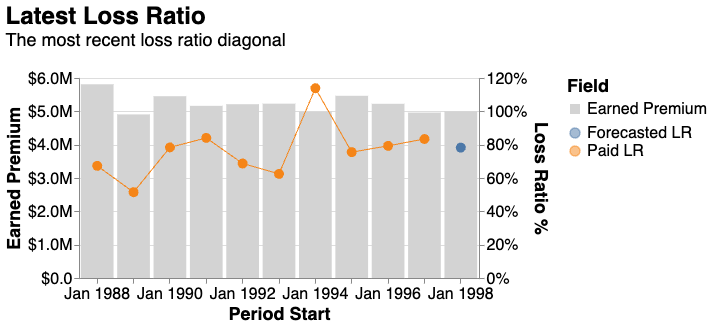
We can compare this to a more sophisticated model, like the SSM model. This model is a bayesian state-space model that incorporates a mean-reverting latent loss ratio.

ssm_forecast = client.forecast_model.create(
   triangle="full_meyers",
   name="ssm_forecast",
   model_type="SSM",
   config={
       "loss_definition": "paid",
   }
)
ssm_prediction = ssm_forecast.predict("full_meyers", target_triangle=target)
ssm_prediction_tri = ssm_prediction.to_bermuda()
ssm_loss_ratio = ssm_prediction_tri[0]['paid_loss'] / ssm_prediction_tri[0]['earned_premium']

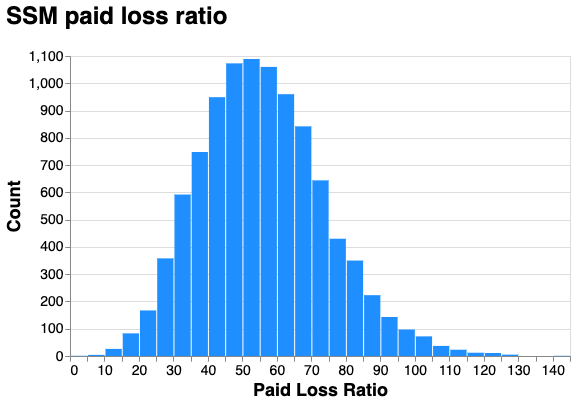
Note that the ssm_loss_ratio is a posterior distribution of 10,000 samples of the ultimate loss ratio unlike the GCC point estimate.